4. Structures d’index: le hachage

Les tables de hachage sont des structures très couramment utilisées en mémoire centrale pour organiser des ensembles et fournir un accès performant à ses éléments. Le hachage est également utilisé par les SGBD pour organiser de grandes collections de données sur mémoire persistante. Une technique intermédiaire, le hachage hybride, consiste à créer une seule structure de hachage dont les données sont partiellement en mémoire RAM et partiellement sur le disque. Le hachage hybride est notamment utilisé pour des algorithmes de jointures sophistiqués sur lesquels nous reviendrons.

Dans ce chapitre nous étudions les structures de hachage utilisées pour indexer de grandes collections de données. La plus simple, le hachage statique ne fonctionne correctement que pour des collections de tailles fixes, ce qui exclut des tables évolutives (le cas le plus courant). Le hachage dynamique, qui s’adapte à la taille de la collection indexée, est présenté en section 2. Il repose sur un répertoire (directory) dont la taille peut croître au point de devenir un problème. Enfin la troisième section introduit le hachage linéaire, une structure qui apporte toute l’efficacité du hachage tout en maintenant une taille de répertoire réduite.

S1: le hachage statique

Supports complémentaires:

• Diapositives du hachage statique:

• Vidéo d’introduction au hachage

Nous commençons par rappeler les principes du hachage avant d’étudier les spécificités apportées par le stockage en mémoire secondaire.

Principes de base

L’idée de base du hachage est d’organiser un ensemble d’éléments d’après une clé, et d’utiliser une fonction (dite de hachage) qui, pour chaque valeur de clé \(c\), donne l’adresse \(f(c)\) d’un espace de stockage où l’élément doit être placé. En mémoire principale cet espace de stockage est en général une liste chaînée, et en mémoire secondaire séquence de blocs sur le disque que nous appellerons fragment (bucket en anglais).

Prenons l’exemple de notre ensemble de films, et organisons-le avec une table de hachage sur le titre. Pour simplifier, on va supposer que chaque fragment contient un seul bloc avec une capacité d’au plus quatre films. L’ensemble des 16 films occupe donc au moins 4 blocs. Pour garder un peu de souplesse dans la répartition qui n’est pas toujours uniforme, on va affecter 5 fragments à la collection de films, et on numérote ces fragments de 0 à 4.

Chaque fragment a une adresse, celle de son premier bloc. Il nous faut donc une structure qui associe le numéro du fragment à son adresse. Cette struture est le répertoire de la table de hachage. Le répertoire est un simple tableau à deux dimensions, avec les numéros dans une colonne et les adresses dans une autre. Le répertoire d’une structure de hachage est en principe très petit et doit tenir en mémoire RAM.

Maintenant il faut définir la règle qui permet d’affecter un film à l’un des fragments. Cette règle prend la forme d’une fonction qui, appliquée à un titre, va donner en sortie un numéro de fragment. Cette fonction doit satisfaire les deux critères suivants:

• le résultat de la fonction, pour n’importe quelle chaîne de caractères, doit être une adresse de fragment, soit pour notre exemple un entier compris entre 0 et 4;

• la distribution des résultats de la fonction doit être uniforme sur l’intervalle \([0, 4]\); en d’autres termes les probabilités d’obtenir chacun des 5 chiffres pour une chaîne de caractères quelconque doivent être égales.

Si le premier critère est relativement facile à satisfaire, le second soulève quelques problèmes car l’ensemble des chaînes de caractères auxquelles on applique une fonction de hachage possède souvent des propriétés statistiques spécifiques. Dans notre exemple, l’ensemble des titres de film commencera souvent par « Le » ou « La » ce qui risque de perturber la bonne distribution du résultat si on ne tient pas compte de ce facteur. On sait définir des fonctions de hachage uniforme, à base d’un savant triturage de la représentation binaire de clés pour éliminer toute régularité. On va supposer ce point acquis: nos fonctions de hachage sont uniformes.

Nous allons utiliser un principe simple pour notre exemple, en considérant la première lettre du titre, et en lui affectant son rang dans l’alphabet. Donc a vaudra 1, b vaudra 2, i vaudra 9, etc. Ensuite, pour se ramener à une valeur entre 0 et 4, on prendra simplement le reste de la division du rang de la lettre par 5 (« modulo 5 »). En résumé la fonction \(h\) est définie par:

\[h(titre) = rang(titre[0])\, mod\, 5\]

La Fig. 4.1 montre la table de hachage obtenue avec cette fonction. Tous les films commençant par a, f, k, p, u et z sont affectés au bloc 1 ce qui donne, pour notre ensemble de films, Annie Hall, Psychose et Underground. les lettres b, g, l, q et v sont affectées au bloc 2 et ainsi de suite. Notez que la lettre e a pour rang 5 et se trouve donc affectée au bloc 0.

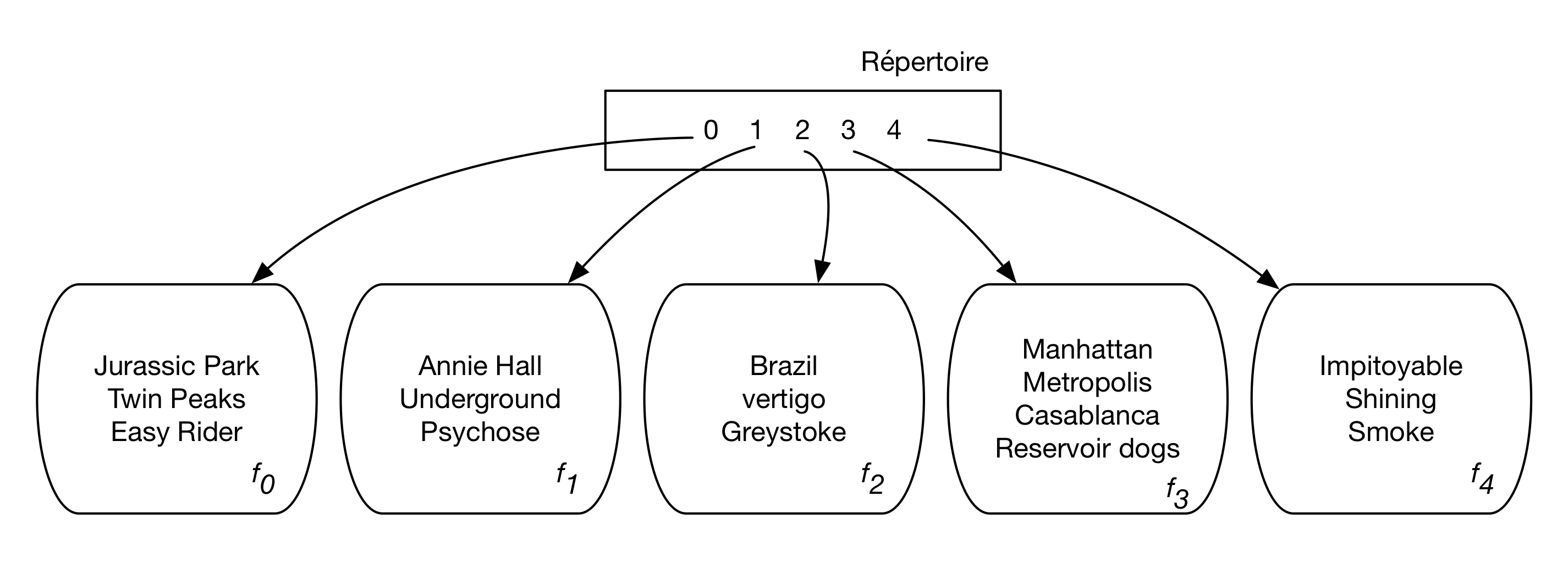
Fig. 4.1 Exemple d’une table de hachage

La Fig. 4.1 présente, outre les cinq fragments \(f_0, \cdots, f_4\) stockant des films, le répertoire à cinq entrées permettant d’associer une valeur entre 0 et 4 à l’adresse d’un fragment sur le disque. Ce répertoire fournit une indirection entre l’identification logique du bloc et son emplacement physique, selon un mécanisme déjà rencontré dans la partie du chapitre Dispositifs de stockage consacrée aux techniques d’adressage de blocs. Comme déjà indiqué, on peut raisonnablement supposer que sa taille est faible et qu’il peut donc résider en mémoire principale, même pour de très grandes structures de hachage avec des milliers de fragments.

On est assuré avec cette fonction d’obtenir toujours un chiffre entre 0 et 4, mais en revanche la distribution risque de ne pas être uniforme: si, comme on peut s’y attendre, beaucoup de titres commencent par la lettre l, le bloc 2 risque d’être surchargé. et l’espace initialement prévu s’avèrera insuffisant.

Dans le pire des cas, une fonction de hachage mal conçue affecte tous les enregistrements à la même adresse, et la structure dégénère vers un simple fichier séquentiel (cas d’une fonction renvoyant toujours à par exemple). Il faudrait utiliser un calcul beaucoup moins sensible à ce genre de biais; prendre par exemple les 4 ou 8 premiers caractères de la chaînes, traiter ces caractères commes des entiers dont on effectue la somme, définir la fonction sur le résultat de cette somme.

Recherche dans une table de hachage

La structure de hachage permet les recherches par titre. Reprenons notre exemple favori:

select *
from Film
where titre = 'Impitoyable'

Pour évaluer cette requête, il suffit d’appliquer la fonction de hachage à la première lettre du titre, i, qui a pour rang 9. Le reste de la division de 9 par 5 est 4, et on peut donc charger le fragment 4 et y trouver le film Impitoyable. On a donc pu effectuer cette recherche en lisant un seul bloc, ce qui est optimal. Cet exemple résume les deux avantages principaux d’une table de hachage:

• La structure n’occupe aucun espace disque additionnel aux données elles-mêmes, contrairement à l’arbre-B;

• elle permet d’effectuer les recherches par clé par accès direct (calculé) au fragment susceptible de contenir les enregistrements.

Sauf exception (ici la recherche par la première lettre du titre), la recherche par préfixe n’est plus possible. La hachage ne permet pas non plus d’optimiser les recherches par intervalle, puisque l’organisation des enregistrements ne s’appuie pas sur l’ordre des clés. La requête suivante par exemple ne peut être résolule que par le parcours de tous les blocs de la structure, même si trois films seulement sont concernés.

select *
from  Film
where titre betseen 'Annie Hall' and 'Easy Rider'

Cette incapacité à effectuer efficacement des recherches par intervalle doit mener à préférer l’arbre-B dans tous les cas où ce type de recherche est envisgeable. Si la clé est par exemple une date, il est probable que des recherches seront effectuées sur un intervalle de temps, et l’utilisation du hachage peut s’avérer un mauvais choix. Mais dans le cas, fréquent, où on utilise une clé séquentielle pour identifier les enregistrements pas un numéro indépendant de leurs attributs, le hachage est tout à fait approprié car une recherche par intervalle ne présente alors pas de sens et tous les accès se feront par la clé.

Mises à jour

Si le hachage peut offrir des performances sans équivalent pour les recherches par clé, il est – du moins dans la version simple que nous présentons pour l’instant – mal adapté aux mises à jour. Prenons tout d’abord le cas des insertions: comme on a évalué au départ la taille de la table pour déterminer le nombre de blocs nécessaire, cet espace initial risque de ne plus être suffisant quand des insertions conduisent à dépasser la taille estimée initialement. La seule solution est alors de chaîner de nouveaux fragments.

Cette situation est illustrée dans la figure Fig. 4.2. On a inséré un nouveau film, Citizen Kane. La valeur donnée par la fonction de hachage est 3, rang de la lettre “c” dans l’alphabet, mais le bloc 3 est déjà plein.

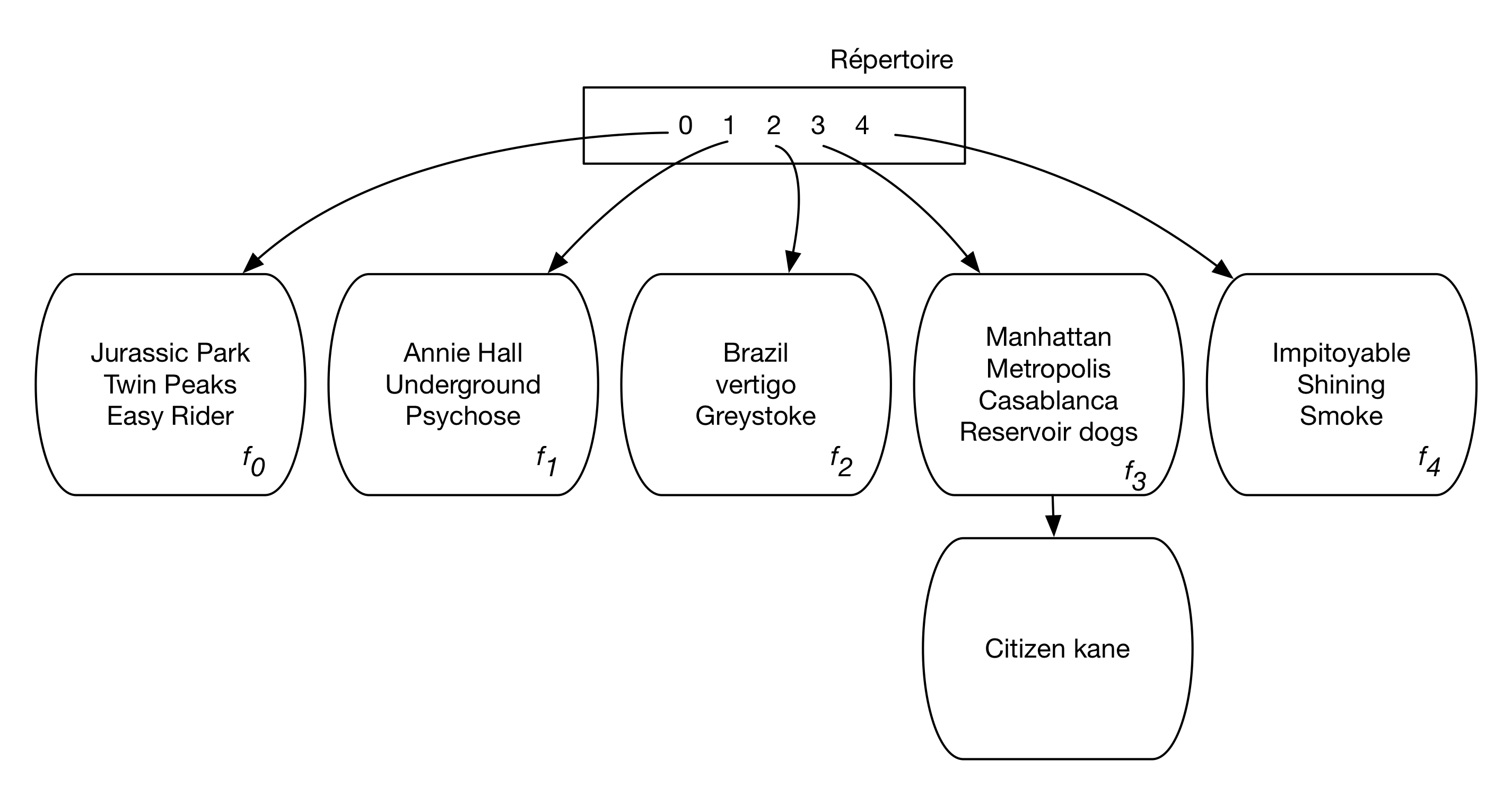
Fig. 4.2 Table de hachage avec page de débordement

Il est impératif pourtant de stocker le film dans l’espace associé à la valeur 3 car c’est là que les recherches iront s’effectuer. On doit alors chaîner un nouveau fragment au fragment 3 et y stocker le nouveau film. À une entrée dans le répertoire, correspondant à l’adresse logique 3, sont associés maintenant deux fragments physiques, avec une dégradation potentielle des performances puisqu’il faudra, lors d’une recherche, suivre le chaînage et inspecter tous les enregistrements pour lesquels la fonction de hachage donne la valeur 3.

Il est très important de noter qu’il est impossible, avec les principes exposés ci-dessus, de modifier la structure de hachage en ajoutant des fragments et en modifiant le répertoire. Cela impliquerait en effet la modification de la fonction de hachage elle-même. On aurait donc une différence entre la fonction utilisée pour le stockage et celle utilisée pour la recherche.

Supposez que l’on ajoute un fragment, la fontion de hachage devient \(modulo(rang, 6)\). La recherche du film “Impitoyable” avec cette fonction nous dirigerait vers le fragment 3 et on ne trouverait pas le film. Toute modification de la fonction de hachage rend la structure obsolète, et il faut la reconstruire entièrement.

Autrement dit, ce type de hachage n’est pas dynamique et ne permet pas, d’une part d’évoluer parallèlement à la croissance ou décroissance des données, d’autre part de s’adapter aux déviations statistiques par rapport à la normale. Il faudrait reconstruire périodiquement la structure en fonction de son évolution. C’est un défaut majeur par rapport à la réorganisation dynamique de l’arbre B.

En résumé, les avantages et inconvénients du hachage statique, comparé à l’arbre-B, sont les suivantes:

• Avantages,: (1) recherche par accès direct, en temps constant; (2) n’occupe pas d’espace disque.

• Inconvénients: (1) pas de recherche par intervalle; (2) pas de dynamicité.

Il n’est pas inutile de rappeler qu’en pratique la hauteur d’un arbre B est de l’ordre de 2 ou 3 niveaux, ce qui relativise l’avantage du hachage. Une recherche avec le hachage demande une lecture, et 2 ou 3 avec l’arbre B, ce qui n’est pas vraiment significatif, surtout quand l’arbre B réside en mémoire RAM. Cette considération explique que l’arbre B, plus généraliste et presque aussi efficace, soit employé par défaut pour l’indexation dans tous les SGBD relationnels.

Enfin signalons que le hachage est une structure plaçante, et qu’on ne peut donc créer qu’une seule table de hachage pour un ensemble de données, les autres index étant obligatoirement des arbres B.

Il existe des techniques plus avancées de hachage dit dynamique qui permettent d’obtenir une structure plus évolutive. La caractéristique comune de ces méthodes est d’adapter le nombre d’entrées dans la table de hachage de manière à ce que le nombre de blocs corresponde approximativement à la taille nécessaire pour stocker l’ensemble des enregistrements. On doit se retrouver alors dans une situation où il n’y a qu’un bloc par entrée en moyenne, ce qui garantit qu’on peut toujours accéder aux enregistrements avec une seule lecture.

Quiz

• À quoi sert le répertoire de la structure de hachage?

  1. À stocker les enregistrements d’après leur clé c

  2. À stocker l’adresse des fragments d’après la valeur de \(h(c)\)

  3. À stocker l’adresse des enregistrements d’après la valeur de \(h(c)\)

  

• Pourquoi la fonction de hachage doit-elle être uniforme?

  1. Parce que les enregistrements doivent être répartis uniformément dans les fragments.

  2. Parce que chaque fragment doit contenir au moins un enregistrement

  3. Parce que deux appels successifs à la fonction doivent toujours donner le même résultat.

  

• Ma clé primaire est un idenfifiant séquentiel. Que peut-on dire du stockage de deux enregistrements dont les clés sont consécutives?

  1. Ils sont dans le même fragment, ou au pire dans deux fragments adjacents.

  2. Ils sont forcément dans deux fragments distincts

  3. Les emplacements des enregistrements sont complètement indépendants.

  

• Quel est, dans le pire des cas, le coût d’une recherche par clé dans une structure de hachage statique?

  1. Dans tous les cas une lecture séquentielle suffit.

  2. Dans le pire des cas tous les fragments sont chaînés et le coût est identique au parcours du fichier

  3. Au pire il faut deux lectures séquentielles, une pour le fragment principal, l’autre pour le fragment chaîné.

  

S2: Hachage extensible

Supports complémentaires:

• Diapositives du hachage extensible:

• Vidéo sur le hachage extensible

Nous présentons tout d’abord le hachage extensible sur un exemple avant d’en donner une description plus générale. Dans un premier temps, la structure est tout à fait identique à celle que nous avons vue précédemment, à ceci près que le nombre d’entrées dans le répertoire est variable, et toujours égal à une puissance de 2.

Maintenant nous supposons donnée une fonction de hachage \(h(c)\) qui s’applique à une valeur de clé c et dont le résultat est toujours un entier sur 4 octets, soit 32 bits. Cette fonction est immuable. Le tableau suivant donne les valeurs obtenues par application de cette fonction aux titres de nos films.

Titre	\(h(titre)\)
Vertigo	01110010
Brazil	1010010
Twin Peaks	11001011
Underground	01001001
Easy Rider	00100110
Psychose	01110011
Greystoke	10111001
Shining	11010011

Comme il n’y a que deux entrées, nous nous intéressons seulement au premier de ces 32 bits, qui peut valoir 0 ou 1. La figure Fig. 4.3 montre l’insertion des cinq premiers films de notre liste, et leur affectation à l’un des deux blocs. Le film Vertigo par exemple a pour valeur de hachage 01110010 qui commence par 0, et se trouve donc affecté à la première entrée.

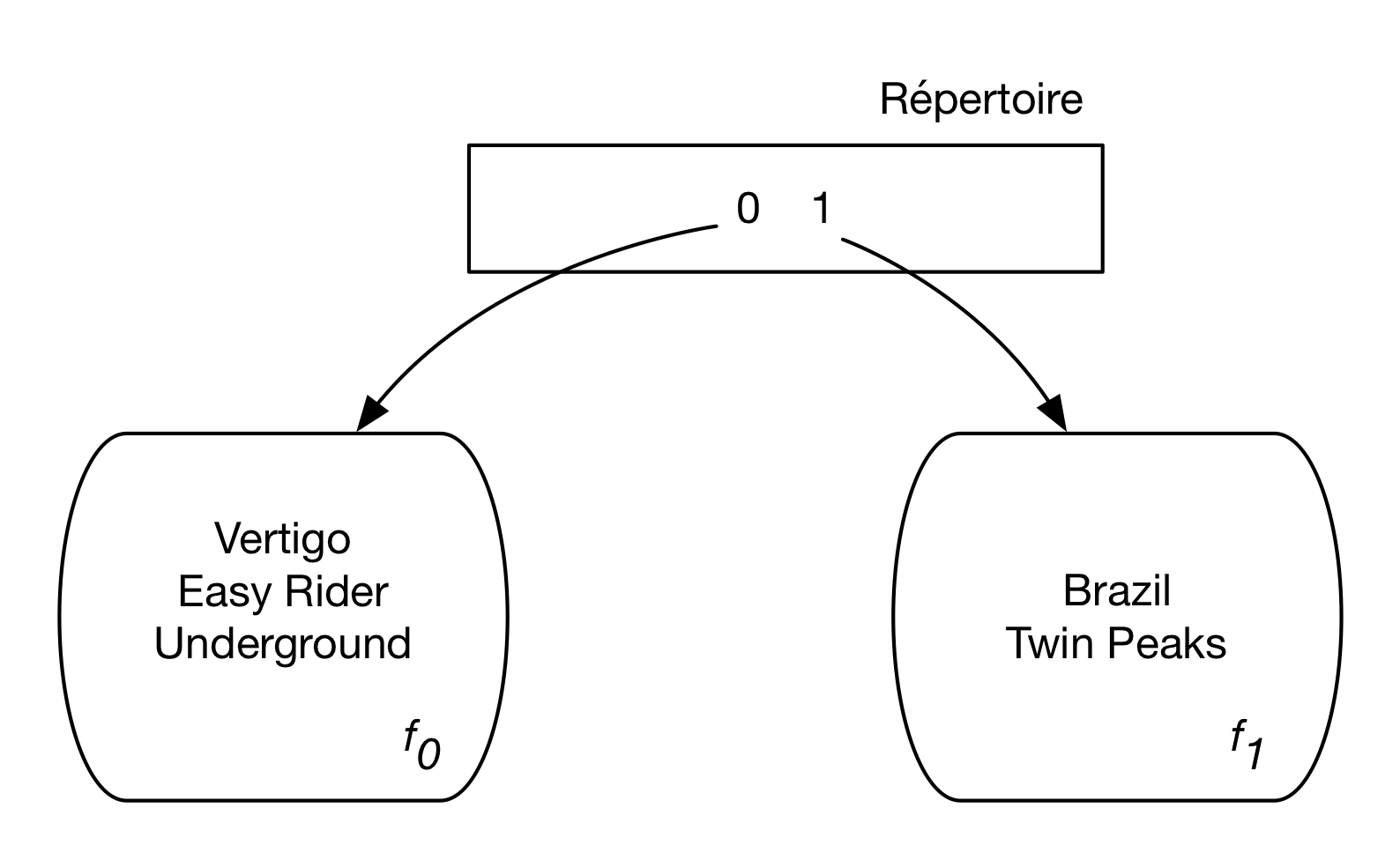
Fig. 4.3 Hachage extensible avec 2 entrées

Supposons, pour la clarté de l’exposé, que l’on ne puisse placer que 3 enregistrements dans un fragment. Alors l’insertion de Psychose, avec pour valeur de hachage 01110011, entraine le débordement du fragment associé à l’entrée 0.

On va alors doubler la taille du répertoire pour la faire passer à quatre entrées, avec pour valeurs respectives 00, 01, 10, 11, soit les \(2^2\) combinaisons possibles de 0 et de 1 sur deux bits. Ce doublement de taille du répertoire entraine la réorganisation suivante (Fig. 4.4):

Fig. 4.4 Doublement du répertoire dans le hachage extensible

En détail:

• les films de l’ancien fragment 0 sont répartis sur les fragments 00 et 01 en fonction de la valeur de leurs deux premiers bits: Easy Rider dont la valeur de hachage commence par 00 est placé dans le premier fragment, tandis que Vertigo, Underground et Psychose, dont les valeurs de hachage commencent par 01, sont placées dans le second fragment.

• les films de l’ancien fragment 1 n’ont pas de raison d’être répartis puisqu’il n’y a pas eu de débordement pour cette valeur,: on va donc associer le même fragment aux deux entrées 10 et 11.

Maintenant on insère Greystoke (valeur 10111001) et Shining (valeur) 11010011. Tous deux commencent par 10 et doivent donc être placés dans le troisième fragment qui déborde alors. Ici il n’est cependant pas nécessaire de doubler le répertoire puisqu’on est dans une situation où plusieurs entrées de ce répertoire pointent sur le même fragment.

On va donc allouer un nouveau fragment à la structure, et l’associer à l’entrée 11, l’ancien fragment restant associé à la seule entrée 10. Les films sont répartis dans les deux fragments, Brazil et Greystoke avec l’entrée 10, Twin Peaks et Shining avec l’entrée 11 (Fig. 4.5).

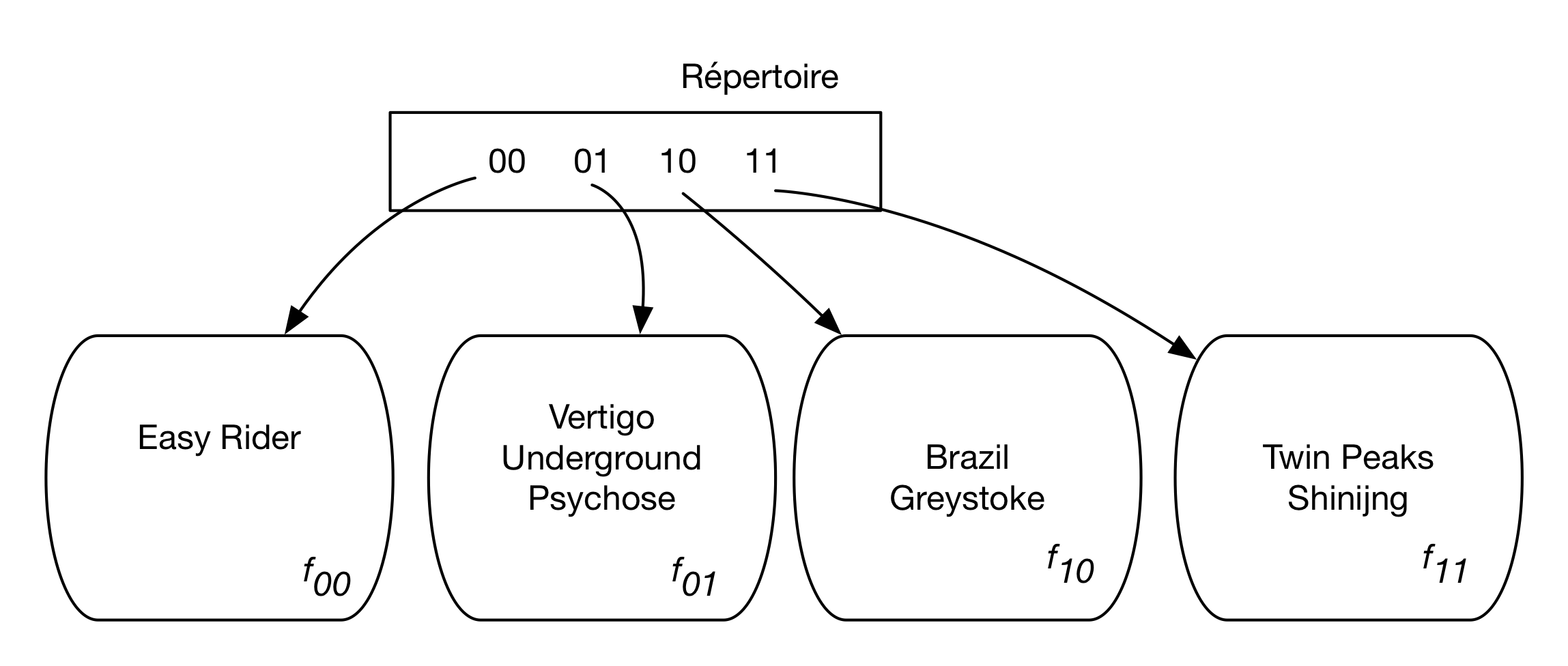
Fig. 4.5 Jeu de pointeurs pour éviter de doubler le répertoire

En résumé, il n’y a que deux cas

• Cas 1: on insère dans un fragment plein, mais plusieurs entrées pointent dessus. On alloue alors un nouveau fragment, et on répartit les adresses du répertoire pour référencer les deux fragments.

• Cas 2: on insère dans un fragment plein, associé à une seule entrée. On double à nouveau le nombre d’entrées

La technique est simple et résout en partir le principal défaut du hachage, l’absence de dynamicité. L’inconvénient potentiel est que le répertoire tend à croître de manière exponentielle, ce qui peut soulever un problème à terme. Le hachage extensible reste par ailleurs une structure plaçante qui doit être complétée par l’arbre B pour des index secondaires.

Quiz

• Qu’est-ce qui caractérise le hachage extensible?

  1. Les fragments sont de taille variable

  2. Le répertoire est de taille variable

  3. La fonction de hachage change régulièrement

  4. On ajoute des fonctions quand la collection grandit

  

• Quelle est la taille maximale du répertoire

  1. \(2^4\)

  2. \(2 \times 4\)

  3. \(2^{32}\)

  4. \(2 \times 32\)

  

• Combien ajoute-t-on de fragments quand l’un deux déborde

  1. un seul

  2. Deux

  3. \(p\) où p est le nombre d’entrée courant dans le répertoire.

  4. Autant que d’enregistrements en trop

  

• Combien d’entrées du répertoire peuvent référencer le même fragment?

  1. une seule

  2. Deux

  3. Autant que nécessaire

  

S3: hachage linéaire

Supports complémentaires:

• Diapositives du hachage linéaire:

• Vidéo de présentation

Le but du hachage linéaire est de maintenir une structure de hachage efficace quand le jeu de données est très dynamique, et en particulier quand il croît très rapidement. Cette maintenance implique une extension progressive du répertoire de hachage et de la fonction de hachage, ainsi que l’ajout de nouveaux fragments. L’apport du hachage linéaire est d’incrémenter à la fois le répertoire et les fragments proportionnellement aux besoins de stockage, et d’éviter le doublement systématique du répertoire.

Le point de départ du hachage linéaire est identique à celui du hachage extensible. Nous supposons donnée une fonction de hachage \(h(c)\) qui s’applique à une valeur de clé c et dont le résultat est toujours un entier sur 4 octets, soit 32 bits. Le tableau suivant donne les valeurs que nous allons utiliser pour illustrer le hachage linéaire sur quelques-uns de nos films.

Titre	\(h(titre)\)
Vertigo	14
Brazil	43
Twin Peaks	25
Underground	20
Easy Rider	8
Psychose	33
Greystoke	17
Shining	16
Citizen Kane	44

La structure est celle d’une table de hachage classique, avec un répertoire dont chaque entrée référence un fragment. Nous prenons comme point de départ la situation de la Fig. 4.6 qui ressemble en tous points à celle du hachage extensible, à une (petite) exception près: un paramètre spécial, l’indice de partitionnement est ajouté à la structure. Appelons-le p. Sa valeur initiale est 0.

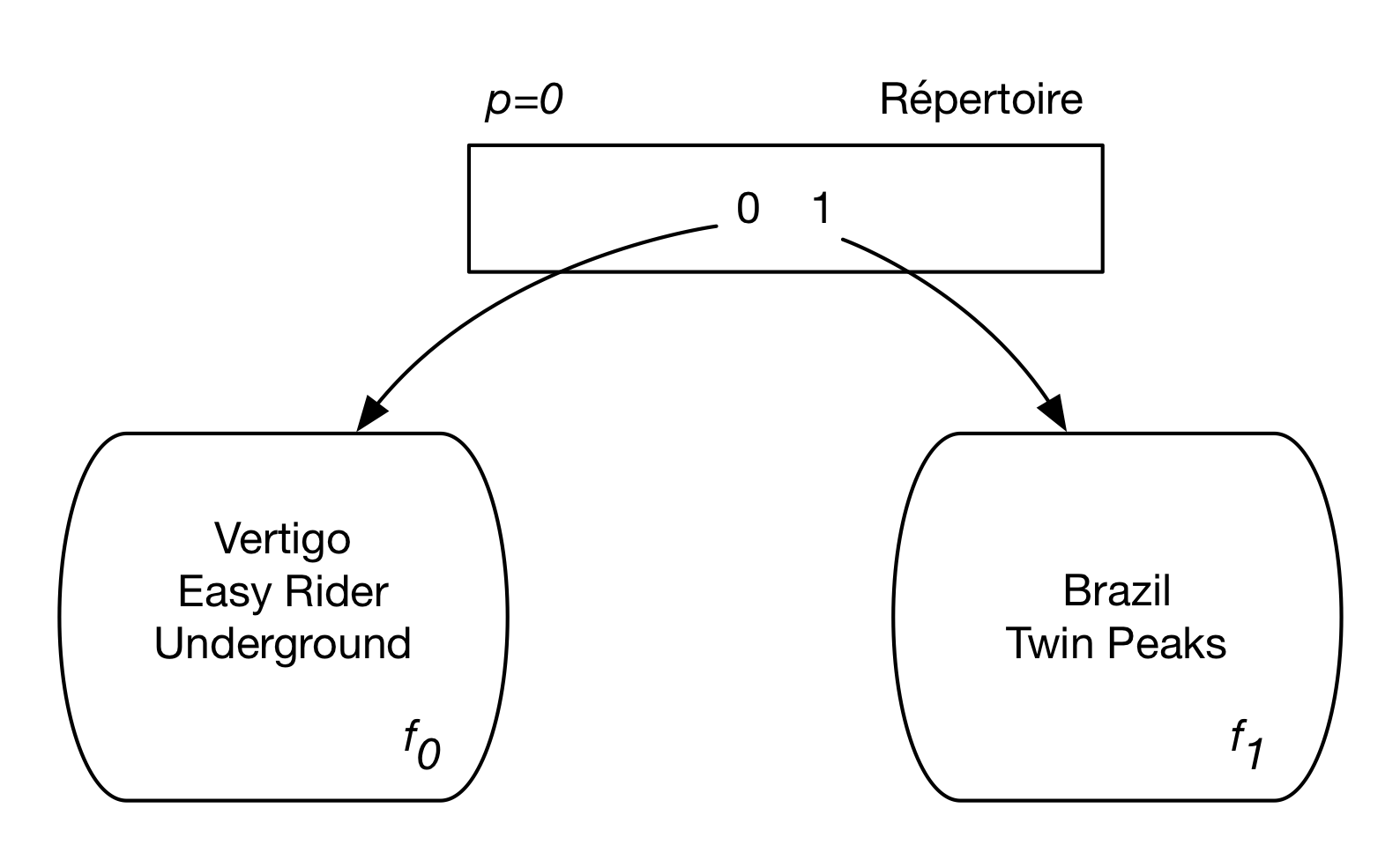
Fig. 4.6 Structure initiale pour le hachage linéaire.

La fonction de hachage utilisée pour la structure de la Fig. 4.6 est \(h(c) \, mod\ 2\), que nous noterons \(h_1\). Plus généralement, on va considérer la suite de fonctions \(h_0, h_1, h_2, \cdots\) définie par

\[h_i (c) = h(c)\, mod\, 2^i\]

En français: le résultat de \(h_i(c)\) est le reste de la division de \(c\) par \(2^i\).

Quand un fragment \(f_i\) déborde, les actions suivantes sont effectuées.

• Un bloc de débordement est chaîné à \(f_i\) pour stocker le nouvel enregistrement.

• Le fragment \(f_p\) est éclaté en (\(f_p\), \(f'_p\)), son contenu réparti dans les deux nouveaux fragments (\(f_p\), \(f'_p\)), et p est incrémenté de 1.

Regardons ce qui se passe après insertion de Psychose, puis de Easy Rider. Tous les deux ont des valeurs impaires pour \(h(c)\) et sont donc placés dans le fragment \(f_1\) qui déborde. Parallèlement à ce débordement, le fragment \(f_0\) est éclaté et son contenu réparti entre \(f_0\) et un nouveau fragment \(f_2\), comme le montre la Fig. 4.6.

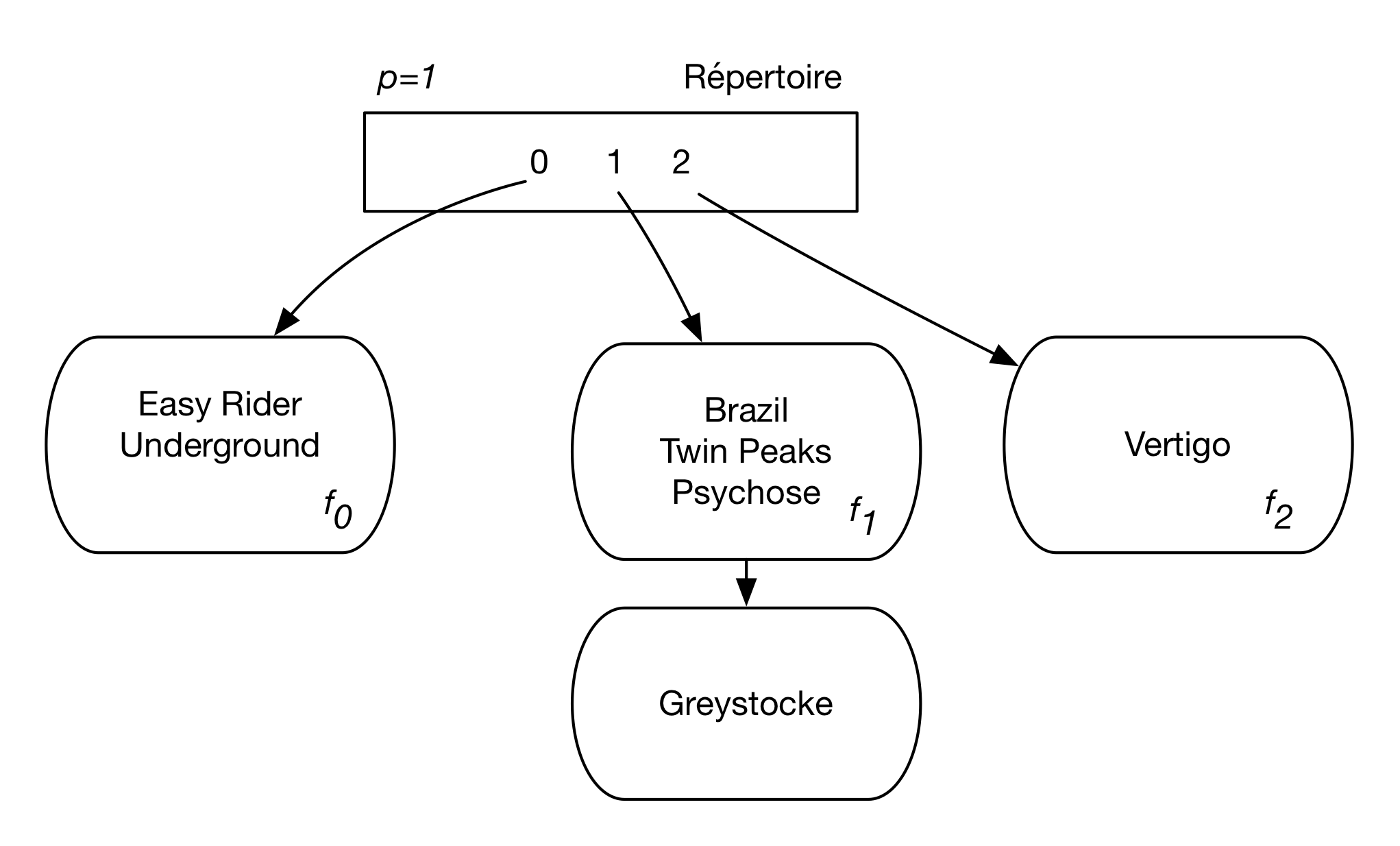
Fig. 4.7 Après débordement de \(f_1\) et éclatement de \(f_0\)

En éclatant le fragment \(f_0\), on a utilisé comme fonction de répartition le successeur de \(h_1\), \(h_2\), et pris donc en compte le reste de la division par \(2^2=4\). Underground et Easy Rider, dont les valeurs respectives de \(h(c)\) sont 24 et 8, restent donc dans \(f_0\), tandis que Vertigo (valeur 14, avec pour reste de la division 2) est déplacé dans \(f_2\).

À ce stade, on constate donc que deux fonctions de hachage cohabitent: \(h_1\) et \(h_2\). Comment savoir laquelle utiliser? Le critère est simplement déterminé par le paramètre p. Le hachage linéaire repose toujours sur une paire de fonctions \((h_n, h_{n+1})\). Initiallement, cette paire est \((h_0, h_1)\), et comme p=0, \(h_0\) s’applique à tous les fragments. Au fur et à mesure de l’évolution de la structure suite à des éclatements, p est incrémenté et \(h_0\) s’applique seulement aux fragments dont l’indice est supérieur ou égal à p, et \(h_1\) à tous les autres.

Continuons notre exemple en insérant successivement Shining (valeur 16) puis Citizen Kane (valeur 48). Tous deux vont dans \(f_0\) qui déborde. Il faut donc éclater le fragment désigné par la valeur courante de p, \(f_1\), et incrémenter p. On se retrouve dans la situation de la Fig. 4.8.

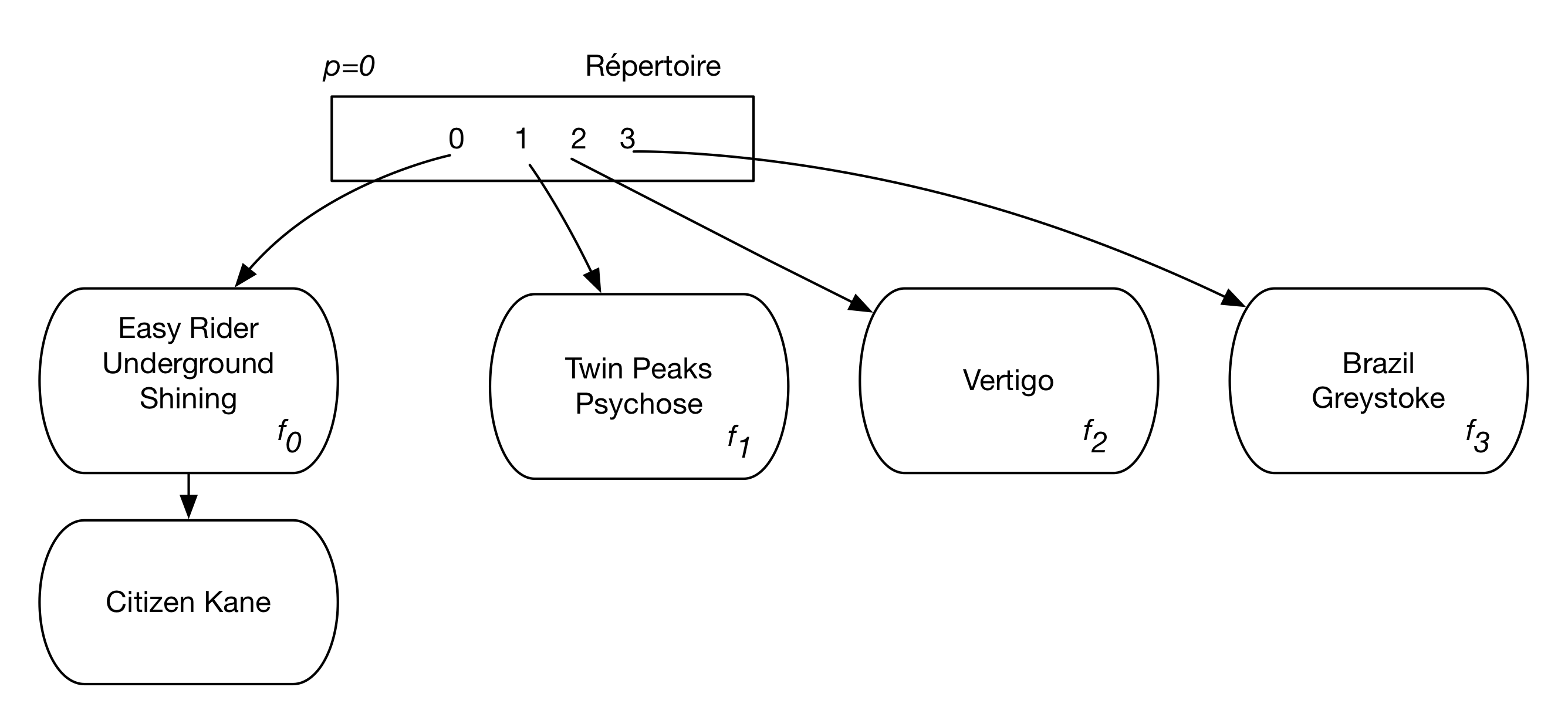
Fig. 4.8 Après débordement de \(f_0\) et éclatement de \(f_1\)

Que constate-t-on? La structure a un nouveau bloc de débordement, mais celui de \(f_1\) a disparu. Pourquoi? Parce qu’en incrémentant p, la fonction \(h_1\) s’applique maintenant à \(f_1\), ce qui conduit à répartir les enregistrements initialement présents soit dans \(f_1\) (si le modulo 4 de la clé est 1) ou le nouveau fragment \(f_3\) (si le modulo 4 et 3).

Résumons. Dans la structure de hachage linéaire, quand un fragment déborde, un nouveau fragment est chaîné. On se retrouve dans la situation du hachage statique, le chaînage introduisant une indirection pénalisante pour les recherches. Si on s’en tenait là il n’y aurait aucun progrès. Mais le hachage linéaire va plus loin en incrémentant également le nombre de valeurs de hachage et effectuant un éclatement de l’un des fragments de la structure, mais pas forcément de celui qui vient de déborder. En fait, le débordement d’un fragment agit comme une sorte de signal que la structure doit évoluer et s’agrandir, et on le fait mais dans un ordre déterminé à l’avance. C’est ce découplage entre la constatation d’un débordement d’un côté, et l’éclatement d’un fragment de l’autre, qui constitue l’idée - brillante - fondant l’organisation du hachage linéaire.

On accepte donc d’avoir des blocs de débordement, mais uniquement de manière temporaire, car, à terme, le fragment qui a débordé et consiste en plusieurs blocs chaînés sera éclaté à son tour, et le chaînage disparaitra. On peut interpréter le principe comme étant celui d’une désynchronisation entre la croissance des données et le nécessaire éclatement des fragments.

On peut noter également qu’après cet éclatement, \(h_0\) n’est plus utilisé. La paire de fonction requises pour la structure devient \((h_1, h_2)\) et p est réinitialisé à 0: on va recommencer une séquence d’éclatement des fragments, en partant de 0, dans l’ordre. Toutes les puissances de 2, on « décale » d’un niveau la paire de fonction de hachage, et on dispose de toutes les informations nécessaires pour gérer les insertions et les recherches. Le petit code suivant est à la base de l’identification du fragment contenant un enregistrement de clé c, la paire courante de fonctions étant \((h_n, h_{n+1})\).

$a := h_n(h(c));
if ($a < $p)  $a := h_{n+1}(h(c))

En clair: on applique d’abord \(h_n\), en supposant que le fragment concerné n’a pas encore éclaté. On obtient une valeur de hachage a. Si a est inférieure à p, c’est :math:` h_{n+1}` qu’il faut utiliser.

Quiz

• Quelle affirmation est vraie pour le hachage linéaire?

  1. Il n’y a jamais besoin de chaîner des fragments en cas de débordement

  2. C’est toujours le même fragment qui éclate

  3. L’éclatement des fragments suit un ordre indépendant des insertions

  

• Comment sait-on quelle fonction de hachage s’applique à une clé?

  1. C’est déterminé en fonction de p

  2. Le milieu du répertoire constitue la frontière

  3. C’est déterminé par la valeur de la clé

  

• Pourquoi accepte-t-on de faire des chaînages dans le hachage linéaire?

  1. Parce qu’ils sont inévitables

  2. Parce qu’ils sont temporaires et vont disparaître à l’occasion d’un futur éclatement

  3. Parce qu’ils n’entraînent pas de problème de performance dans le cas du hachage linéaire.

  

Exercices

Exercice ex-hach1: construction d’un hachage statique

Reprenons une liste de 12 départements, à lire de gauche à droite et de bas en haut.

3  Allier; 36 Indre; 18 Cher; 75 Paris
39 Jura; 9  Ariège; 81 Tarn; 11 Aude
12 Aveyron; 25 Doubs; 73 Savoie; 55 Meuse;

La clé étant le numéro de département et on suppose qu’un bloc contient 5 enregistrements.

• Proposez une fonction de hachage et le nombre d’entrées du répertoire, puis construisez une structure de hachage statique en prenant les enregistrements dans l’ordre indiqué.

Correction

Il y a 12 départements, donc à priori on peut se contenter de 3 pages et il reste un peu de place. Pour la fonction de hachage, on prend simplement \(c\mod 3\) où c est le code du département.

La table de hachage est donnée par la Fig. 4.9. On constate un fort déséquilibre et une page de débordement, dues à la répartition non uniforme des numéros de département dans notre échantillon.

Fig. 4.9 Le hachage statique, montrant une répartition non uniforme des enregistrements

Exercice ex-hach2: avec hachage extensible

Même exercice, mais avec une structure basée sur le hachage extensible. La fonction de hachage est la suivante: \(h(nom) = i_1 i_2 \cdots i_4\) avec \(i_j = 1\) si la lettre \(nom[i_j]\) est en position impaire dans l’alphabet, et 0 sinon. Donc \(f(Aude)=1101\). Voici la liste des valeurs de hachage, en ne prenant que les 4 premiers bits.

Allier  1001    Indre   1000    Cher    1010    Paris   0101
Jura    0101    Ariège  1011    Tarn    0100    Aude    1101
Aveyron 1011    Doubs   0110    Savoie  1101    Meuse   1111

• On suppose toujours 5 enregistrements par bloc. Choisissez le nombre de bits initial de la structure de hachage en fonction du nombre de départements à indexer, et donnez la structure obtenue.

• Prenez les départements suivants, dans l’ordre indiqué (de gauche à droite, puis de haut en bas) et donnez les évolutions de la structure de hachage extensible.

  Cantal  1100    Marne   1100    Loire   0110    Landes  0100
  Calvados 1110   Gard    1110    Vaucluse 0111   Ardèche 0011
  

Correction

Il y a 12 enregistrements, il faut au moins 3 blocs donc on va prendre en compte les deux premiers bits, avec quatre valeurs possibles et 4 blocs.

La structure est donnée dans la Fig. 4.10. Notre fonction n’est toujours pas uniforme et aucun département n’est placé dans \(f_0\) (cela viendrait sûrement).

Fig. 4.10 Situation initiale du hachage extensible, en prenant 2 bits pour 12 départements

Continuons les insertions comme indiqué dans l’énoncé. Le Cantal et la Marne vont tous les deux dans le fragment \(f_{11}\), la Loire et les Landes dans le bloc \(f_{01}\) qui déborde alors.

Il faut éclater \(f_{01}\) en \(f_{010}\) et \(f_{011}\). Il n’est réféerencé que par une seule entrée dans le répertoire, il faut donc doubler la taille de ce dernier. Tous les autres fragments sont alors référencés par 2 entrées (Fig. 4.11).

Fig. 4.11 Après éclatement de \(f_{01}\)

Insérons maintenant le Calvados. Cette fois c’est \(f_{110}\) qui est plein et doit être éclaté entre \(f_{110}\) et \(f_{111}\). Comme \(f_{110}\) était référencé par deux entrées, il est inutile de doubler le répertoire. la Fig. 4.12 montre la structure finale.

Fig. 4.12 Situation finale

Exercice ex-hach3: un peu de hachage linéaire

Expliquez l’évolution du hachage linéaiere en partant de la Fig. 4.8 et en insérant deux films, Metropolis donc le code de hachage est 49, et Manhattan donc le code est 5.

Correction

Les deux films vont dans le fragment \(f_{1}\) qui déborde. On crée donc un bloc de débordement. Comme p=0, c’est \(f_{0}\) qui éclate, donnant naissance à \(f_{4}\). Les enregistrements initialement présents dans \(f_{0}\) sont répartis et le chaînage disparaît. La valeur de p devient 1 (=numref:hachExo3).

Fig. 4.13 Le hachage linéaire après insertion de Metropolis et Manhattan

Donc

• le prochain fragment à éclater sera \(f_{1}\), et le chaînage disparaîtra à cette occasion

• \(h_3\), qui applique un modulo 8, s’applique aux recherches dans les fragments avant \(f_{1}\)

• \(h_2\) s’applique aux autres recherches.